La matematica di Perseverance

Con qualche calcolo possiamo renderci conto della fisica che controlla la discesa di una sonda su un altro pianeta e prevederne la velocità di arrivo al suolo

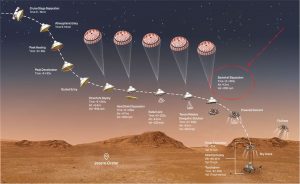
Abbiamo ancora tutti negli occhi lo spettacolare video dell’atterraggio della sonda Perseverance sul pianeta rosso, avvenuto pochi giorni fa. Il robot è stato infatti sganciato dall’orbita marziana e si sono apprezzate diverse fasi nella discesa verso la superficie, tra cui una intermedia avvenuta con un paracadute.

Già, un “semplice” paracadute. Il bello della scienza è che le leggi che pensiamo governino la realtà ed i fenomeni siano universali, funzionano cioè allo stesso modo qui sulla Terra, su Marte ed in qualunque altro luogo dello spazio. Ciò che varia sono semplicemente i parametri al contorno ma il “motore” alla base del fenomeno che vediamo è lo stesso.

Per questo motivo, sebbene sia tecnicamente molto più complicato, la fisica che regola l’atterraggio di un paracadutista sulla Terra è la stessa che regola l’atterraggio di Perseverance su Marte.
Ma come cambia allora nel “paracadutarsi” su Marte e come differisce invece che dalla Terra ? Vediamolo un po’ più in dettaglio, sfruttando il fatto che come abbiamo detto, la fisica è la stessa e cambiano solo i dati “al contorno” 😊. Ovviamente non abbiamo la pretesa di confronto con il grandissimo lavoro della NASA e dei suoi scienziati, semplicemente pensiamo sia bellissimo mostrare come con una spiegazione molto approssimata e con poche formule di poche considerazioni, si riesca ad intuire come possa un oggetto complesso atterrare su Marte.

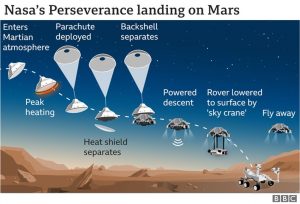
In fisica la somma di tutte le forze che agiscono su un corpo porta un corpo a spostarsi se la risultante di queste forze non è nulla. Con uno schema, significa questo nel nostro caso di Perseverance:

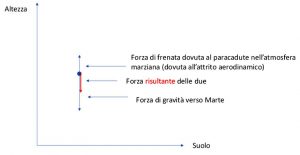
L’oggetto quindi scende perché la forza di gravità verso Marte è più forte della frenata provocata dall’attrito con l’atmosfera marziana. Se non fosse così, vedremo l’oggetto allontanarsi da Marte invece che scenderci sopra 😊

Sappiamo quindi che nel cadere, l’oggetto prende via via sempre più velocità. Viene appunto accelerato dalla forza di gravità che lo spinge a cadere sempre più velocemente. A questo punto interviene la frenata dovuta al paracadute ed all’attrito che tutto questo oggetto ha con l’atmosfera marziana. Questa forza è però un pochino diversa dalla gravità: diventa più forte man mano che l’oggetto ha una velocità elevata. A bassa velocità invece non ha praticamente effetti importanti.

In poche parole e riassumendo, più Perseverance precipita verso la superficie di Marte, tanto più acquista velocità per effetto della gravità, tanto più la forza frenante del paracadute diventa forte e tende a rallentarlo (nei primi istanti la frenata è molto violenta). Continuando a decelerare, giunge un momento in cui la forza di gravità e la frenata aereodinamica si equivalgono. A quel punto l’oggetto cade con una velocità costante, che in fisica si chiamata “velocità limite”. Oltre questo valore quindi la gravità non aumenta il suo effetto ed il paracadute non basta più per frenare completamente l’oggetto. E’ per questo che nell’ultima fase, la frenata finale avviene con dei motori esterni.

Vediamo più in dettaglio le forze in gioco che abbiamo finora introdotto:

• Forza di gravità su Marte: è la stessa formula della forza che abbiamo sulla Terra, ma con una g più piccola, essendo Marte più piccolo della Terra

• Perseverance ha una massa totale di circa 1025 Kg (https://www.media.inaf.it/2020/04/23/bilanciando-perseverance/)

• gMarte è di circa 3,71 m/s²

• La forza aerodinamica di resistenza dell’atmosfera è invece la seguente:

• costante di resistenza aerodinamica, dipende da molti fattori tra cui generalmente questi sono quelli da considerare:
  • Coefficiente di resistenza aerodinamica C_r: approssimando Perseverance in prima battuta ad una sfera (vedendo infatti la superficie di protezione sferica di impatto del robot), questo valore è di circa 0,47 (https://it.wikipedia.org/wiki/Coefficiente_di_resistenza_aerodinamica)

• Densità dell’atmosfera marziana ρ: circa cento volte minore della Terra, quindi circa 12,9 grammi/m³ (sulla Terra siamo a circa 1,3 kg/m³)

• Area della superficie di attrito A: il paracadute di Perseverance ha un diametro di 21,5 mt (https://mars.nasa.gov/mars2020/timeline/landing/entry-descent-landing/)

Globalmente, la K ha come valore 0,2141 dato dalla formula:

Questo valore dipende fortemente dalle condizioni di Marte: il pianeta ha pochissima atmosfera e molto poco densa.

• V(t) è invece l’andamento della velocità del corpo nel tempo. Vediamo da questo punto come al crescere della velocità, la forza frenante aumenta con il quadrato della velocità.

Il principio della risultante delle forze in fisica unita al secondo principio della dinamica di Newton (F=m*a) ci porta a scrivere questa formula risultante:

(il sistema di riferimento che abbiamo scelto, con l’origine al suolo e puntando verso l’alto ci dice che la forza di gravità e quella risultante hanno il segno “–“ perché sono discendenti).

Cioè, in termini più chiari:

Usando i termini precedenti diventa:

L’equazione sopra riportata è un’equazione differenziale, un tipo di equazioni il cui risultato non è un numero bensì una formula. Nel nostro caso, la formula che ricerchiamo è la v(t), cioè l’andamento della velocità di Perseverance man mano che questa cade sotto l’effetto della gravità e della frenata del paracadute. Sappiamo che il paracadute è stato aperto quando la velocità di discesa aveva raggiunto una Viniziale = 1512 km/h dopo circa 240 secondi (6 minuti) dall’inizio della discesa (https://mars.nasa.gov/mars2020/timeline/landing/entry-descent-landing/). Con questa informazione che rappresenta le cosiddette “condizioni iniziali al contorno”, la matematica ci permette di risolvere analiticamente ed esattamente l’equazione e troviamo che la soluzione è data dalla seguente formula:

dove:

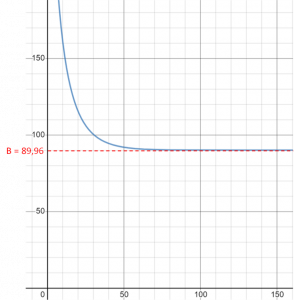
Il segno negativo della velocità indica sempre che Perseverance è in discesa verso il riferimento posto sul suolo marziano. L’andamento di questa funzione è (in valore assoluto) il seguente:

Figura 1 Asse Y = velocità; Asse X = tempo

Secondo le previsioni di questa formula, calcolata con metodi di basilari di analisi, possiamo vedere che per tempi t >> A, ad esempio dopo 100 secondi, la velocità dell’oggetto è prossima a -B, cioè 89,96 m/s, che corrisponde a circa 323,8 km/h che equivalgono a 201 mph. In altre parole, in circa 100-110 secondi la frenata dovuta al paracadute ha sortito il suo effetto ed usandolo per tempi più lunghi non porterebbe alcun ulteriore beneficio frenante. Confrontiamo questo valore con i dati reali diffusi dalla NASA:

Dalla figura vediamo che in effetti la velocità limite raggiunta con il paracadute è di 200 miglia orarie come calcolato e che sono passati esattamente 350-240 = 110 secondi dall’apertura del paracadute.

I dati coincidono in modo quasi perfetto!

Riepilogando, ecco quindi che dei quasi 8 minuti dovuti alla fase più violenta della discesa, i primi 6 sono stati usati per la caduta libera, mentre gli ultimi due sono stati usati per frenare con il paracadute (fino a circa 320 km/h) e poter ristabilire il contatto radio con la Terra. Infine, l’ultima fase della discesa avviene tramite ulteriori fasi di rallentamento operate da motori esterni, fino al punto di frenare del tutto la capsula e poi far scendere il robot Perseverance finalmente sul suolo marziano tramite un verricello alla velocità finale di circa 3 km/h.

Ma possiamo fare di più…! Dalle leggi della dinamica newtoniana sappiamo infatti che possiamo dedurre facilmente l’accelerazione (o meglio, la decelerazione nel nostro caso) di un oggetto conoscendo la formula della sua velocità. E’ infatti sufficiente calcolarne la derivata temporale di tale funzione ed otterremo il tasso di decelerazione di Perseverance. Applicando quindi le leggi matematiche di derivazione, otteniamo la formula della decelerazione:

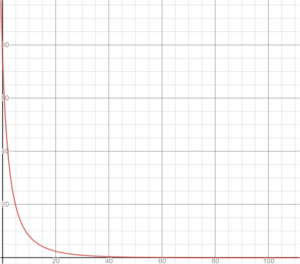
Come nel caso precedente, anche per questo possiamo farne un grafico del suo andamento:

Figura 2 Asse Y = Accelerazione/Decelerazione; Asse X = tempo

Vediamo che al tempo t=0, cioè all’apertura del paracadute, abbiamo una decelerazione di circa 85-90 m/s² di frenata. Tale decelerazione corrisponde ad un valore di circa 9 g di frenata che sussiste nei primi secondi dall’apertura del paracadute. Dall’andamento del grafico vediamo che gran parte della frenata avviene nei primi 10-15 secondi, dove Perseverance passa dai 9 g ad un valore di 1 g.

Dalla letteratura pubblicata dalla NASA sull’atterraggio di Perseverance vediamo che ancora una volta le semplici previsioni dei nostri calcoli si sono rivelate accurate!

https://www.washingtonpost.com/science/2021/02/18/mars-landing-nasa/

https://www.jpl.nasa.gov/news/nasas-mars-perseverance-rover-provides-front-row-seat-to-landing-first-audio-recording-of-red-planet

Piccola curiosità: le g calcolate sono “g terrestri”….ma su Marte la gravità non è così forte come sulla Terra perché è un pianeta più piccolo: una decelerazione di 9 “g terrestri” corrisponde invece a circa 24 “g marziane”!

A cura di Mattia Antonio Musella

Febbraio 2021